I was discussing procedural content with someone last week and I was reminded of some research into space filling distributions and their use in games. One interesting procedure that I’ve run across is called the Halton Sequence, and it has some interesting properties. It’s space filling, deterministic, and pseudo-random. As such, it’s not only great for distributing things seemingly at random over a surface, but the objects will never overlap and can be made to cluster. You can read a nice description of how it was used in the game Spore from Maxis’ 2007 Game Developer Conference presentation.
It’s not a terribly efficient sequence generation algorithm if you’re generating them on the fly, but if you know you’ll need a block of them it’s much more efficient to generate a table at a time. This is because the distribution function requires the previously generated value to calculate the next – similar to a Fibonacci sequence. You can create multiple distributions because one of the input parameters is a prime number, thus it’s easy to generate 2D, 3D, etc. sequences just by providing different primes for each dimension you need.
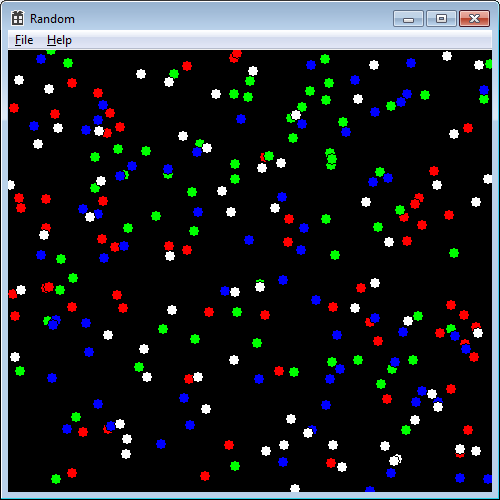
It’s better if we look at it in action. Let’s look at a random distribution of 256 points via rand(). The first quarter generated are red, the second are blue, the third green, the fourth white.
You get the random scattering you’d expect, with some too near or even intersecting each other.
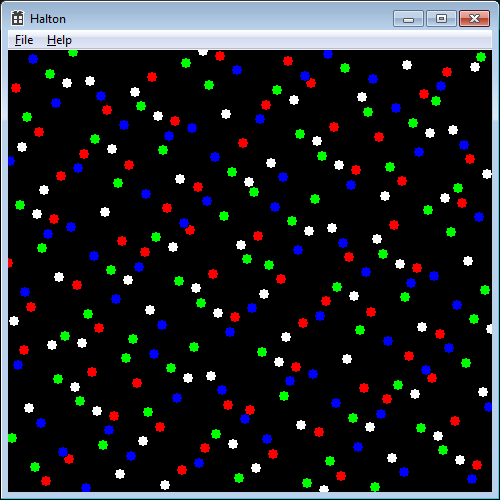
Now let’s use a Halton Sequence with a prime of 2 for the horizontal distribution and 3 for the vertical with the same colorization scheme.
See how much more evenly distributed the colors are? And how “later” colors are clustered around earlier one? You can use this to distribute “types” evenly and cluster objects around them – for example trees in the first pass, then – continuing with the same Halton Sequence – tall bushes, then following that, still using the same sequence – shorter shrubs, then grasses. The Halton sequence will prevent them from overlapping but they will fill in space around already placed objects.
It’s not quite that easy in practice, but it gets you 95% of the way there, and with some filtering techniques and some care about the primes you use (some start off too well ordered – see the Wikipedia article) you can put the generation tools in the hands of your artists and generate tons of seeming naturally ordered, yet randomized procedurally grouped content. YMMV – will require some tweaking to get that last 5%.
And it’s not just geometric objects you can place, but NPCs (or clusters of NPCs), loot, terrain features — you can even use it to procedurally generate features in texture maps (like spots on a leopard, etc. ). I love procedurally generated content, and this is one of the tools I use to get great looking environments.
OK – what does the code look like – here’s a very simple and unoptimized version – you start off with some seed index value (zero works initially) along with a prime number as the base, then you increment the index value with that same prime to generate the next number in the sequence.
.
// A simple Halton Sequence generation routine
// indx is the starting value for the sequence (0 or 1 is always good)
// and base is a prime number.
// Increment indx value for the next value in the sequence.
float halton(int indx, int base)
{
float b = (float)base;
float i = (float)indx;
float h = 0.0f, digit = 0.0f, f = 1.0f/b;
while (i>0)
{
digit = (int)i % base;
h += digit * f;
i = (i-digit) / b;
f /= b;
}
return(h);
}
.
It’s not efficient to generating each number one at a time, but it works. A better way is to have it generate an array sequentially using results to continue to the next value in the sequence – this is a much more efficient calculation. Then you can generate batches of numbers with much less overhead (or have some state residing the the sequence generator).