I’m going to start some posts on how to “Let The Computer Figure It Out”. I see rational folks sometimes use trial and error to figure something out – a totally valid methodology – but occasionally there’s a need for either responding to a dynamic system in code or just plain not taking advantage of the fact that you have a frikkin computer at your disposal and there’s no need NOT to let if do the math for you. There are a few techniques that will enable you to just let the computer figure it out for you. This is the first one.
It turns out that it’s fairly easy to code these implementations in software, and today I’m going to discuss one of the basic and most useful controller equations – that of the Proportional-Integral-Derivative controller, or PID controller.
Occasionally you need to fine tune some parameters according to changing conditions – you basically want something that will adjust to meet a set of conditions. I frequently see folks make educated guesses and try to get values that are in the ballpark of being acceptable. This works for one-off’s but it’s really simple to get a computer to fine tune things for you. In my Chemical Engineering past I learned about control theory, and it turns out that these techniques are frequently used in other fields as well, from many engineering fields, some AI fields, financial, and pretty much anywhere there’s a need for mechanical controllers. Physical PID controllers are all around us – while computer implementations are frequently used for everything from smart thermostats, HVAC systems, robotics, AI’s to drive cars, missile targeting systems, etc. Anywhere you need to have a system to respond to changing conditions, you can probably use a PID controller.
A PID controller is used when you have a output value that (typically) responds to some adjustment value – think of it as a dial where you can turn the dial and make the output value go up or down. The PID controller is given control of the dial and monitors the output. If the output deviates from the desired target value (called the setpoint), the controller will adjust the dial. Here’s the equation for a PID controller.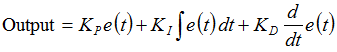
The value e(t) is the error or deviation of the actual output from the setpoint as a function of time. The three parts on the right side are (in order) the proportional, derivative, and integral – hence the PID name. The K values are the controller constants, and adjust how much of each part of the PID equation contributes to the final value – and are how the PID controller is adjusted to be responsive.
The Proportional Control
The proportional control is basically how much the dial gets turned when there is an error in the output value. It’s directly proportional to the difference between the setpoint and the actual value – for some cases you can just use the error directly and set the control and you’re done – but particularly in either physical systems or dynamic computer systems, you will be constantly adjusting the setpoint to adjust the output to new conditions, and that’s when the rest of the PID terms come into play. If you think about a hot water tank, the heat comes on till the water reaches the setpoint, then the heat shuts off. Residual heat will raise the temperature a bit more, overshooting the setpoint – but since we can’t cool the water, we need to wait for it to naturally lose heat till we start to accumulate a significant error, at which point the heat will kick on again. Hot water tanks and your home heating systems are a special sort of controller situation – typically called bang-bang controllers – because they have a state of being on or off (hence bang-bang) with no other states – thus they are just P controllers, with no adjusting of the controls other than on or off. The proportional part is the main contributor to the controller value – it’s Proportional to the error. The larger the error, the larger the adjustment to the controller.
The Integral Control
The integral part is the part of the PID equation takes into account any steady-state or constant forces that are changing the output value – like heat loss in a water tank, or trying to aim at a moving target. The integral part is actually the integration of the error values over time – thus it’s a value that provides adjustment to the controller if there’s a build up of error over time. A controller can be a PI controller, and in many cases this is good enough. The proportional part will make the gross adjustments, the integral part can keep a small part of the controller active to offset any bias in the system.
The Derivative Control
The derivative part can be considered the part that rapidly adjusts to a change in the error – the derivative part serves to adjust the direction of the control – hence when the error goes from positive to negative (e.g. we just moved through the setpoint value) the derivative changes sign and serves to damp down any oscillations in the controller. The derivative part is frequently used when the process changes rapidly and you want the setpoint to be very closely monitored and need the controller to be very quick to adjust. However, if you have a noisy system, including derivative may make things worse.
Summary
Now a PID controller has one input and one output – but frequently you can use a bunch of them in tandem to control more than just one value. It’s even common to have PID controller values feeding into other PID controllers when you have a more complicated process to control. Next time – the code.